Solving large Markov Chains¶
| Date: | 2008-12-28 (last modified), 2008-12-28 (created) |
|---|
This page shows how to compute the stationary distribution pi of a large Markov chain. The example is a tandem of two M/M/1 queues. Generally the transition matrix P of the Markov chain is sparse, so that we can either use scipy.sparse or Pysparse. Here we demonstrate how to use both of these tools.
Power Method¶
In this section we find pi by means of iterative methods called the Power method. More specifically, given a (stochastic) transition matrix P, and an initial vector pi_0, compute iteratively pi_n = pi_{n-1} P until the distance (in some norm) between pi_n and pi_{n-1} is small enough.
Fist we build the generator matrix Q for the related Markov chain. Then we turn Q into a transition matrix P by the method of uniformization, that is, we define P as I - Q/l, where I is the identity matrix (of the same size as Q) and l is the smallest element on the diagonal of Q. Once we have P, we approximate pi (the left eigenvector of P that satisfies pi = pi P) by the iterates pi_n = pi_0 P\^n, for some initial vector pi_0.
More details of the above approach can be found in (more or less) any book on probability and Markov Chains. A fine example, with many nice examples and attention to the numerical solution of Markov chains, is `Queueing networks and Markov Chains' by G. Bolch et al., John Wiley, 2nd edition, 2006.
You can get the source code for this tutorial here: tandemqueue.py
#!/usr/bin/env python
labda, mu1, mu2 = 1., 1.01, 1.001
N1, N2 = 50, 50
size = N1*N2
from numpy import ones, zeros, empty
import scipy.sparse as sp
import pysparse
from pylab import matshow, savefig
from scipy.linalg import norm
import time
This simple function converts the state (i,j), which represents that the first queue contains i jobs and the second queue j jobs, to a more suitable form to define a transition matrix.
def state(i,j):
return j*N1 + i
Build the off-diagonal elements of the generator matrix Q.
def fillOffDiagonal(Q):
# labda
for i in range(0,N1-1):
for j in range(0,N2):
Q[(state(i,j),state(i+1,j))]= labda
# mu2
for i in range(0,N1):
for j in range(1,N2):
Q[(state(i,j),state(i,j-1))]= mu2
# mu1
for i in range(1,N1):
for j in range(0,N2-1):
Q[(state(i,j),state(i-1,j+1))]= mu1
print "ready filling"
In this function we use scipy.sparse
def computePiMethod1():
e0 = time.time()
Q = sp.dok_matrix((size,size))
fillOffDiagonal(Q)
# Set the diagonal of Q such that the row sums are zero
Q.setdiag( -Q*ones(size) )
# Compute a suitable stochastic matrix by means of uniformization
l = min(Q.values())*1.001 # avoid periodicity, see the book of Bolch et al.
P = sp.speye(size, size) - Q/l
# compute Pi
P = P.tocsr()
pi = zeros(size); pi1 = zeros(size)
pi[0] = 1;
n = norm(pi - pi1,1); i = 0;
while n > 1e-3 and i < 1e5:
pi1 = pi*P
pi = pi1*P # avoid copying pi1 to pi
n = norm(pi - pi1,1); i += 1
print "Method 1: ", time.time() - e0, i
return pi
Now use Pysparse.
def computePiMethod2():
e0 = time.time()
Q = pysparse.spmatrix.ll_mat(size,size)
fillOffDiagonal(Q)
# fill diagonal
x = empty(size)
Q.matvec(ones(size),x)
Q.put(-x)
# uniformize
l = min(Q.values())*1.001
P = pysparse.spmatrix.ll_mat(size,size)
P.put(ones(size))
P.shift(-1./l, Q)
# Compute pi
P = P.to_csr()
pi = zeros(size); pi1 = zeros(size)
pi[0] = 1;
n = norm(pi - pi1,1); i = 0;
while n > 1e-3 and i < 1e5:
P.matvec_transp(pi,pi1)
P.matvec_transp(pi1,pi)
n = norm(pi - pi1,1); i += 1
print "Method 2: ", time.time() - e0, i
return pi
Output the results.
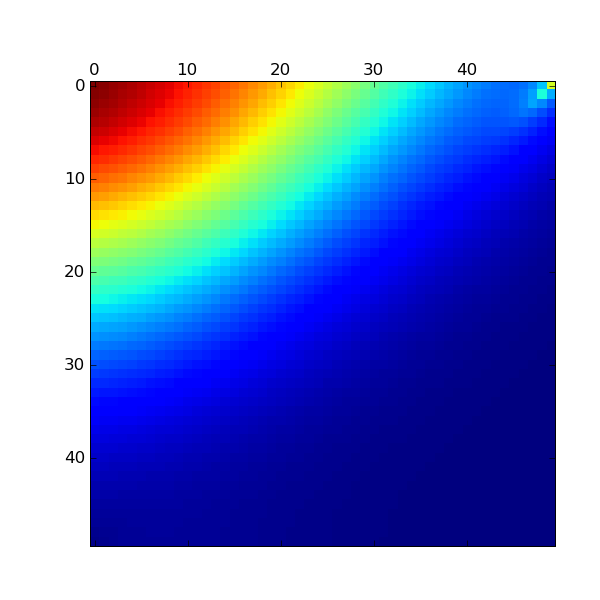
def plotPi(pi):
pi = pi.reshape(N2,N1)
matshow(pi)
savefig("pi.eps")
if __name__ == "__main__":
pi = computePiMethod1()
pi = computePiMethod2()
plotPi(pi)
Here is the result:
Improvements of this Tutorial¶
Include other methods such as Jacobi's method or Gauss Seidel.
Section author: nokfi
Attachments